Winter School in Мathematics and Theoretical Computer Science January 29 – February 3, 2021

The school is held jointly by the Faculty of Mathematics of HSE and the Faculty of Mathematics and Computer Science of St. Petersburg State University. The school consists of a number of mini-courses and aims to overview various topics in mathematics and theoretical computer science. We invite senior undergraduate students who plan to continue their studies in theoretical mathematics, as well as graduate students.  

When: January 29 - February 3, 2021  
Where: Zoom


List of mini-courses.

Petr Dunin-Barkowski (NRU HSE): Hurwitz-type numbers and their generating functions

 Hurwitz numbers have been studied since the 19th century. The original numbers introduced by Adolf Hurwitz (nowadays called the "simple Hurwitz numbers") have a very simple combinatorial definition: a given Hurwitz number corresponds to the number of ways of representing a permutation of a given cyclic type as a product of a fixed number of transpositions. Hurwitz was motivated to study these numbers due to the fact that they appear in a geometric context, counting ramified coverings of a two-dimensional sphere. There are many interesting generalizations and modifications of the concept of Hurwitz numbers, including double Hurwitz numbers, monotone and strictly monotone Hurwitz numbers, Bousquet-Mélou--Schaeffer numbers and many more. All these Hurwitz-type numbers, in fact, come from the so-called tau-functions of hypergeometric type of the Kadomtsev-Petviashvili (KP) integrable hierarchy. As part of this course, we will discuss the basic definitions and properties of various Hurwitz-type numbers (both from the purely combinatorial and from the geometric sides), with examples. 
Then we will briefly mention the relation to the KP hierarchy (no prior knowledge of integrable systems is required, all notions will be explained), and then we will discuss the interesting properties of generating functions of Hurwitz-type numbers. In particular, it turns out that in full generality the natural generating functions of these Hurwitz-type numbers can be represented as finite rational expressions in certain basic functions.

The continuum hypothesis states that any infinite subset of reals has the cardinality of either natural numbers or reals. In 1963 Cohen showed the statement to be independent of the ZFC axioms of set theory, that is, neither the statement nor its negation could be deduced from the axioms. A sheaf on a topological space X is a local homeomorphism into X. The category of sheaves on a space gives a model of set theory, so one can deduce independence of hypotheses by proving statements about sheaves. Developing on this idea allows one to reprove Cohen's result. In these lectures we will discuss these ideas and this proof and if time permits we will also talk a bit about type theory.

Viacheslav Borovitskiy (SPbSU): Gaussian random fields in machine learning

Gaussian random fields (Gaussian processes) are beautiful and rather well-studied mathematical objects that are useful in a number of areas outside of pure mathematics. In machine learning, they are widely accepted as a model of choice in scenarios where decision making under uncertainty is required e.g. in geological modeling, black-box optimization and robotics. In these lectures we will discuss Gaussian process models in machine learning. Specifically, we will talk about the efficient algorithms to fit Gaussian process models to data and to make predictions with them. We will also explore their applications in geostatistics, optimization and reinforcement learning.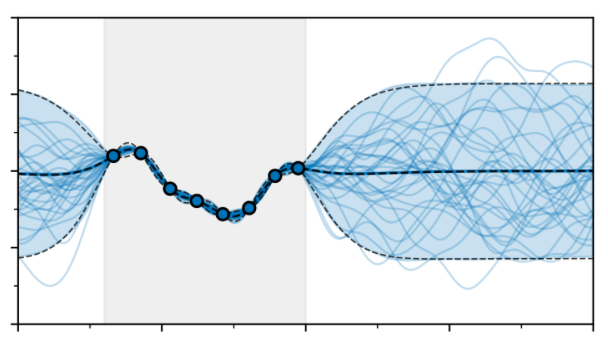
 

Dmitriy Stolyarov (SPbSU) On isomorphism of some Banach spaces

I will tell two classical, but nearly forgotten, stories from functional analysis, namely, from the Banach space theory. The first concerns the Milyutin Theorem (1952). It says that for any uncountable metrizable compact sets $K_1$ and $K_2$, the Banach spaces $C(K_1)$ and $C(K_2)$ are isomorphic (i.e., there exists a linear homeomorphism between them). The second story will be about Henkin’s theorem which states that there is no isomorphism between $C^1([0,1]^2)$ and $C([0,1]^2)$.

  Alexander Tiskin  (SPbSU)  Efficient parallel algorithms   Slides (PDF, 3.96 Mb) 

Parallel computation, which has been a narrowly specialised topic until fairly recently, is fast becoming the mainstream of computer science. Parallelism brings about a new level of complexity that creates the need for new theoretical approaches to its understanding. In addition to the time spent on computation itself, we now have to consider inter-processor communication and synchronisation; other important aspects are memory efficiency and fault tolerance. The course will consider the main existing models of parallel computation, with a particular emphasis on the model of bulk-synchronous parallelism (BSP), proposed by Leslie Valiant in 1990. A BSP computation consists of a sequence of asynchronous local computation blocks, interleaved with blocks of communication and barrier synchronisation. Valiant proved that this class of parallel computation can be implemented efficiently with a very simple randomised routing algorithm. At the same time, this class is sufficiently broad to serve as a basis for the design of efficient parallel algorithms. We will study the main design principles of BSP algorithms looking at several classical problems: sorting and selection, fast Fourier transform, list ranking, grid computations, matrix multiplication, linear system solution, string comparison, finding shortest paths in a graph. For most of these problems, a naive parallelisation is possible; however, optimal solutions, taking communication and synchronisation costs into account, are often non-trivial and instructive.

Alexei Pirkovskii (NRU HSE)       Noncommutative complex analysis: selected topics       (in Russian) 
Vladimir Bogachev (MSU & NRU HSE)       Spaces of measures and optimal transportation       (in Russian) 
Leonid Rybnikov (NRU HSE)       Robinson–Schensted–Knuth correspondence in algebra and geometry       (in Russian)

 
Records of the talks
Questions can be addressed to Andrey Dymov.