Проекты факультета математики

Список книг, рекомендованных для чтения факультетом математики НИУ ВШЭ

 

---

Dubrovin's superpotential as a global spectral curve

В работе доцента факультета математики П.И.Дунина-Барковского

Dunin-Barkowski, P.; Norbury, P.; Orantin, N.; Popolitov, A.; Shadrin, S.

Dubrovin's superpotential as a global spectral curve. J. Inst. Math. Jussieu   18(2019), no. 3, 449–497,

написанной в соавторстве с профессорами П.Норбури (Мелбурн), Н.Орантэн (Париж), С.Шадриным (Амстердам) и   научным сотрудником А.Пополитовым получен ряд важных результатов, лежащих на стыке ряда математических дисциплин, таких как топология, алгебраическая геометрия, математическая физика, теория поля. Результаты работы имеют важные приложения как в самой математике, так и математической физике. В частности, авторами описаны взаимосвязи между теорией суперпотенциалов Ландау-Гинзбурга, фробениусовыми структурами Дубровина и активно развивающейся в настоящее время теорией топологической рекурсии для спектральных кривых.  Кроме того, в работе получен способ построения когомологических теорий поля, связанных с фробениусовыми многообразиями, в терминах разложения корреляционных дифференциалов. Полученные результаты имеют важное значение для современной математической физики и позволят продвинуться в ряде недоступных до этого направлениях.  Все полученные авторами результаты опубликованы в  статье в журнале Journal of the Institute of Mathematics of Jussieu, который публикует самые влиятельные статьи по всем областям математики и является одним из ведущих международных рецензируемых журналов по математике в мире.

 

A_n - особенности, 1 ≤ n ≤  3

 

---

 

Global bifurcations in the two-sphere: a new perspective

В работе профессора факультета математики НИУ ВШЭ Юлия Сергеевича Ильяшенко и доцентов  Юрия Георгиевича Кудряшова  и Ильи Валерьевича Щурова 

"Global bifurcations in the two-sphere: a new perspective"  Yu. Ilyashenko, Yu. Kudryashov, I. Schurov

Inventiones mathematicae (2018), Volume 213, Issue 2, pp. 461–506  

изучаются векторные поля на двумерной сфере. Работа посвящена теории бифуркаций – математической теории, изучающей поведения сложных динамических систем. В статье Ильяенко, Кудряшова и Щурова получено несколько важных результатов. В частности, получен контрпример к гипотезе Арнольда 1985 года о стабильности семейств векторных полей на двумерной сфере. Для этого в работе строится шести-параметрическое семейство векторных полей, топологическая классификация которого обладает функциональным Построенные в статье примеры семейств векторных полей и их инвариантов открывают новые возможности   в глобальной теории бифуркаций. Статья опубликована в журнале Q1  Inventiones mathematicae, который является одним из самых влиятельных и высокоцитируемых журналов по математике в мире: журнал публикует лучшие статьи из всех областей математики.

 

 

 

 

Монодромный полицикл  “сепаратнисная петля” (слева) и немонодромнвй полицикл “средце” (справа)

---

Categorical proof of holomorphic Atiyah-Bott formula

Kondyrev, Grigory; Prikhodko, Artem Categorical proof of holomorphic Atiyah-Bott formula. J. Inst. Math. Jussieu 19 (2020), no. 5, 1739–1763.

Работа посвящена новому доказательству знаменитой формулы Атьи-Ботта, также известной как формула Лефшеца. Эта формула, полученная около 50 лет назад, позволяет вычислять различные характеристики расслоений на многообразиях в локальных терминах. Она оказала огромное влияние на развитие математики последних десятилетий. Г.Кондыреву и А.Приходько удалось получить новое доказательство формулы Атьи-Ботта, применив современную технику теории категорий. Работа опубликована в журнале Journal of the Institute of Mathematics of Jussieu. Этот журнал издаётся издательством Cambridge University Press и является одном из ведущих мировых журналов, публикующем лучшие работы математиков со всего мира.

Авторы применили мощный аппарат современной производной алгебраической геометрии последнего десятилетия для доказательства классической теоремы Атьи-Ботта. Это не только позволило получить новое доказательство знаменитой теоремы, но и открыло возможность использования современной теории категорий в различных приложениях. Результат является чрезвычайно важным для разнообразных конструкций теории категорий, а также может быть применён в различных приложениях в топологии и алгебраической геометрии. Кроме того, разработанные авторами подходы позволят в дальнейшем применять мощные методы современной теории категорий к различным классическим математическим задачам.

 

       Ключевая коммутативная диаграмма:

 

 

---

 

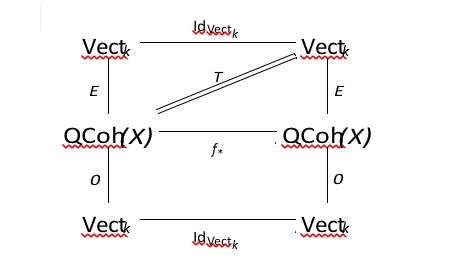
Crystals and monodromy of Bethe vectors

I.Halacheva, J.Kamnitzer, L.Rybnikov, A.Weekes,  Crystals and monodromy of Bethe vectors. Duke Math. J. 169 (2020), no. 12, 2337–2419.

Авторы: Iva Halacheva (Research Instructor,  Northeastern University), Joel Kamnitzer (Professor, University of Toronto), Леонид Рыбников (доцент, НИУ ВШЭ), Alex Weeks (postdoc, University of British Columbia) 

В работе разработаны новые методы изучения  семейств собственных векторов алгебры Годена. Использован мощный современный математический аппарат теории интегрируемых систем, теории пространств модулей кривых, теории представлений алгебр Ли. Авторы доказали ряд теорем о структуре монодромии собственных векторов. В частности, доказана гипотеза Этингофа о согласованности монодромии и действия фундаментальной группы (группы кактуса) на  тензорном произведении кристаллов. 

Работа находится на стыке теории представлений, алгебраической геометрии, комбинаторики и математической физики. Изучаются алгебры Годена, зависящие от точки компактификации Делиня-Мамфорда пространства модулей кривых рода ноль.   Алгебры Годена играют важнейшую роль в теории интегрируемых систем, при этом большая часть информации о той или иной физической системе может быть получена в терминах собственных векторов алгебр Годена.  Авторы получили ряд результатах о поведении семейства собственных векторов  при изменении точки пространства Делиня-Мамфорда. Результат сформулирован в терминах фундаментальной группы (группа кактуса) и кристальных базисов. Работа напечатана в одном из ведущих международных математических журналов Duke Mathematical Journal, входящим в первую пятёрку по общематематическому рейтингу.

Результат может быть применён в различных задачах теории интегрируемых систем, теории представлений конечномерных и аффинных алгебр Ли, комбинаторике кристаллов. Результат является важным, поскольку затрагивает сразу несколько смежных областей современной математики и математической физики. 

Тензорное произведение двух кристаллов   для sl(2):

                      

 

 

---

 

The Gauss–Manin connection on the periodic cyclic homology

Работа профессора факультета математики НИУ ВШЭ  Вадим Александровича Вологодского, студента факультета Александра Петрова и сотрудника Института высших исследований (Принстон, США) Дмитрия Вайнтроба 

The Gauss–Manin connection on the periodic cyclic homology. Alexander Petrov, Dmitry Vaintrob, Vadim Vologodsky. Selecta Mathematica, 2018, Volume 24,Issue 1, pp 531–561

посвящена изучению периодических циклических когомологий гладких аффинных неприводимых кривых. Эта важная область алгебраический геометрии привлекает к себе внимание самых влиятельных математиков со всего мира (Фалтингс, Гетцлер, Каледин). В статье доказано зануление когомологий Хохшильда достаточно высокого порядка (не ниже характеристики основного поля минус два). Кроме того, в работе получено доказательство нильпотентности p-кривизны связности Гаусса-Манина и доказано, что p-кривизна может быть выражена через класс Кодаира-Спенсера. Как следствие доказан аналог локально теоремы монодромии Грффитма-Ландмарка-Гротендика. Статья опубликована в журнале Q1  Selecta Mathematica, который публикует статьи по математике самого широкого профиля, которые в дальнейшем существенным образом повлияют на развитие общемировой математики.

Аналог формулы Каца для p-кривизны связности Гаусса-Манина на когомологиях де Рама: