- A
- A
- A
- АБB
- АБB
- АБB
- А
- А
- А
- А
- А
- Национальный исследовательский университет «Высшая школа экономики»
- Факультет математики
- Зимняя студенческая школа по математике и теоретической информатике. 29 января - 03 февраля 2021 года
-
Факультет
- О факультете
- Цифры и факты
- Прием 2026
- Приём 2025
- Наука
- Информация для сотрудников
- Диссертационный совет
- Международный экспертный совет
- Библиотека
- Наши партнеры
- Выпускники
- Сотрудники
- Арнольдовская стипендия
- Moscow Mathematical Journal
- RUTUBE канал факультета математики
- Видеоматериалы
- Ссылки
- Студенческий совет
-
Образование
- Образование
- Бакалаврские программы
- Магистерские программы
- Аспирантура
- Программа Math in Moscow
- Программы для учителей и школьников
- Майнор «Математические структуры»
- Календарь школ
-
Подразделения
- Базовые кафедры
-
Научные подразделения
-
- Международная лаборатория теории представлений и математической физики ВШЭ
- Международная лаборатория кластерной геометрии
- Лаборатория алгебраической геометрии и ее приложений
- Международная лаборатория зеркальной симметрии и автоморфных форм
- Научно-учебная лаборатория сложных сетей, гиперграфов и их приложений
- Лаборатория математического образования
-
-
In Memoriam
- Мы помним
-
Виртуальная доска объявлений
Адрес: 119048, Москва,
ул. Усачёва, 6
тел. (495) 916-89-05
тел. (495) 772-95-90 *12725
E-mail: math@hse.ru
Учебный офис:
mathstudyoffice@hse.ru
тел. (495) 624-26-16
тел. (495) 772-95-90 *12713
Telegram каналы:
Канал Студсовета Матфака - @mathhse_council
Канал Деканата - @mathhse_news
Канал Учебного офиса ФМ - @mathhse_study
Канал Матфак внеучебка - @mathhse
ДПО факультета математики:
dpo-math@hse.ru
Проект «Математическая вертикаль»:
math.vertical@hse.ru
ЛМШ факультета математики - Летняя школа для школьников:
math.vertical.school@hse.ru
Редакторы сайта факультета:
Зимняя студенческая школа по математике и теоретической информатике. 29 января - 03 февраля 2021 года
Школа проводится совместно факультетом математики НИУ ВШЭ и факультетом математики и компьютерных наук СПбГУ.
Школа состоит из набора миникурсов и ставит своей целью осветить различные направления современной математики и теоретической информатики. Мы приглашаем студентов старших курсов бакалавриата, планирующих продолжить изучение теоретической математики, студентов старших курсов математических и смежных специальностей, а также аспирантов.
Когда: 29 января - 03 февраля 2021 года
Где: онлайн на платформе Zoom
Расписание школы находится здесь.
На указанный вами при регистрации адрес будет выслана ссылка на zoom-конференцию, по которой будут проходить доклады.
Список миникурсов:
А.Ю. Пирковский (НИУ ВШЭ): Некоммутативный комплексный анализ: избранные сюжеты Prikovskii (PDF, 8.94 Мб)
Некоммутативный комплексный анализ --- наука довольно молодая, поэтому он пока не имеет сформированного "ядра", характерного для более зрелых математических дисциплин. Иначе говоря, на данный момент трудно выделить достаточно стабильную совокупность фундаментальных понятий и результатов, которую, по общему соглашению работающих в этой области специалистов, можно было бы назвать основами некоммутативного комплексного анализа (и включить, например, в учебник). Фактически существует несколько точек зрения на то, что именно следует называть некоммутативным комплексным анализом. Они отличаются друг от друга, во-первых, выбором классических объектов, некоммутативные аналоги которых следует строить и исследовать, и во-вторых, "степенью некоммутативности" вводимых объектов. Среди классических объектов комплексного анализа, у которых есть содержательные "некоммутативизации", отметим, во-первых, сами голоморфные функции (рассматриваемые как индивидуальные объекты), алгебры голоморфных функций на различных областях в C^n или на комплексных многообразиях, банаховы (или операторные) алгебры голоморфных функций с определенными свойствами "конечности" (например, ограниченных или равномерно аппроксимируемых многочленами на некотором компакте), комплексные структуры на гладких многообразиях, голоморфные векторные расслоения... Что же касается "степени некоммутативности" соответствующих некоммутативных объектов, то с этой точки зрения некоммутативный комплексный анализ можно довольно грубо поделить на "свободный" и "квантованный". В первом случае "переменные", от которых берутся некоммутативные голоморфные функции, не связаны никакими соотношениями --- более точно это означает, что они порождают свободную ассоциативную алгебру. Во втором случае, напротив, такие соотношения имеются, зависят от некоторого числового параметра q, и при стремлении q к единице превращаются в соотношения коммутирования (так что "квантованный" комплексный анализ в некотором смысле содержит классический в качестве предельного случая). Цель данного миникурса --- дать доступное введение в некоторые направления некоммутативного комплексного анализа и по возможности обсудить взаимосвязи между ними. В частности, будут затронуты следующие сюжеты: голоморфные функции нескольких свободных переменных в духе Винникова и Калюжного--Вербовецкого, алгебры свободных голоморфных функций Тейлора и Попеску, квантовый шар Ваксмана и его некоммутативная граница Шилова (принцип максимума), алгебры голоморфных функций на квантовом полидиске и квантовом шаре, квантовый аналог теоремы Пуанкаре о голоморфной неэквивалентности полидиска и шара (и, возможно, некоторые другие).
В.И. Богачев (МГУ, ВШЭ): Пространства мер и оптимальная транспортировка Основные понятия (PDF, 87 Кб)
П.И. Дунин-Барковский (НИУ ВШЭ): Различные виды чисел Гурвица и их производящие функции
Числа Гурвица изучались с 19-го века. Исходные числа, введенные Адольфом Гурвицем (сейчас их называют "простые числа Гурвица") имеют очень простое комбинаторное определение: число Гурвица соответствует количеству способов представить перестановку данного циклического типа в виде произведения заданного количества транспозиций. Для Гурвица мотивировкой для изучения этих чисел было то, что они возникают в геометрическом контексте как количества разветвленных накрытий двумерной сферы.
Существует много интересных обобщений и модификаций понятия чисел Гурвица, включая двойные числа Гурвица, монотонные и строго монотонные числа Гурвица, числа Буске-Мелу--Шеффера и многие другие. Как выясняется, все эти виды чисел Гурвица приходят из т.н. тау-функций гипергеометрического типа иерархии Кадомцева-Петвиашвили (КП).
В рамках курса будут обсуждены основные определения и свойства различных типов чисел Гурвица (как с чисто комбинаторной, так и с геометрической стороны), с примерами. Затем будет кратко упомянута связь с иерархией КП (для этого от слушателей не потребуется никакого предварительного знания теории интегрируемых иерархий, все необходимые понятия будут объяснены). После этого будут обсуждены интересные свойства производящих функций чисел Гурвица. В частности, оказывается, что для максимально общего вида чисел Гурвица их естественные производящие функции можно представить в виде конечных рациональных выражений от небольшого количества базовых функций.
Комплексные неприводимые представления симметрической группы Sn нумеруются разбиениями числа n (т.е. диаграммами Юнга из n клеток), а размерности этих представлений равны количеству стандартных заполнений соответствующей диаграммы Юнга (т.е. количеству стандартных таблиц такой формы). Согласно общей теореме, сумма квадратов размерностей неприводимых представлений равна порядку группы. Таким образом, множество пар стандартных n-клеточных таблиц Юнга одинаковой формы и множество всех перестановок n-элементного множества равномощны. Соответствие Робинсона-Шенстеда-Кнута (RSK) - это чисто комбинаторный алгоритм, устанавливающий взаимно-однозначное соответствие между этими множествами. С другой стороны, то же самое соответствие возникает из двух разных способов индексации клеток Шуберта на многообразии полных флагов: при помощи перестановок и при помощи пар стандартных таблиц. Я постараюсь подробно разобрать перечисленные выше сюжеты: 1. описание неприводимых представлений симметрической группы, 2. конструкция биекции RSK и 3. клетки Шуберта на многообразии полных флагов), рассказать как они связаны и (если останется время) что-то сказать об их дальнейших обобщениях. Для понимания требуется хорошее знание линейной алгебры и начальные сведения из теории представлений и алгебраической геометрии.
Д.М. Столяров (СПбГУ) Об изоморфизме некоторых банаховых пространств
Я расскажу два классических, но полу-забытых сюжета из функционального анализа, более точно, из теории банаховых пространств. Первый — это теорема Милютина (1952), которая гласит, что для всяких несчётных метрических компактов $K_1$ и $K_2$ банаховы пространства $C(K_1)$ и $C(K_2)$ изоморфны (то есть, существует линейный гомеоморфизм между ними). Второй — теорема Хенкина (1967) о том, что между пространствами $C^1([0,1]^2)$ и $C([0,1]^2)$ такого изоморфизма нет.
А. В. Тискин (СПбГУ): Эффективные параллельные алгоритмы Slides (PDF, 3.96 Мб)Параллельные вычисления, еще относительно недавно бывшие узкоспециализированной темой, стремительно входят в мейнстрим современной компьютерной науки. Новый уровень сложности, привносимый параллелизмом в вычислительный процесс, создает потребность в его теоретическом осмыслении. Наряду с временем, затраченным на собственно вычисления, в качестве ограниченных ресурсов при параллельных вычислениях должны рассматриваться также межпроцессорная коммуникация и синхронизация; кроме того, особое значение приобретает эффективное использование памяти и отказоустойчивость. В курсе будут рассмотрены основные существующие модели параллельных вычислений; основное внимание будет уделено модели bulk-synchronous parallelism (BSP), предложенной Лесли Вэлиантом (Leslie Valiant) в 1990 г. Вычислительный процесс BSP представляет из себя последовательность блоков асинхронных локальных вычислений, чередующихся с блоками коммуникации и барьерной синхронизации. Вэлиант доказал, что этот класс параллельных вычислений может быть эффективно реализован при помощи чрезвычайно простого вероятностного алгоритма маршрутизации. При этом данный класс достаточно широк, чтобы служить основой для разработки эффективных параллельных алгоритмов. Мы изучим основные принципы разработки BSP алгоритмов на примере нескольких классических задач: сортировка и выбор порядковой статистики, быстрое преобразование Фурье, ранжирование списка, вычисления на решетке, умножение матриц, решение системы линейных уравнений, сравнение строк, поиск кратчайших путей в графе. Для большинства этих задач возможно наивное распараллеливание вычислений, однако оптимальные решения, с учетом затрат на коммуникацию и синхронизацию, зачастую нетривиальны и поучительны.
В.А. Соснило (СПбГУ): Пучки и континуум-гипотеза.Континуум-гипотеза утверждает, что любое бесконечное подмножество вещественных чисел равномощно либо натуральным числам, либо вещественным. В 1963-м году Коэн показал, что это утверждение не зависимо от стандартной аксиоматики теории множеств ZFC, то есть ни оно, ни его отрицание не могут быть из неё выведены. Пучок на топологическом пространстве X − это локальный гомеоморфизм из некого пространства в X. Категория пучков на пространстве является моделью для теории множеств, поэтому вопросы независимости гипотез можно решать, доказывая утверждения о пучках. Развитие этой идеи позволяет передоказать результат Коэна. В этом курсе планируется разобрать эти идеи и это доказательство и, если останется время, обсудить вкратце теорию типов.
В.А. Боровицкий (СПбГУ): Гауссовы поля в машинном обучении
Gaussian random fields (Gaussian processes) are beautiful and rather well-studied mathematical objects that are useful in a number of areas outside of pure mathematics. In machine learning, they are widely accepted as a model of choice in scenarios where decision making under uncertainty is required e.g. in geological modeling, black-box optimization and robotics. In these lectures we will discuss Gaussian process models in machine learning. Specifically, we will talk about the efficient algorithms to fit Gaussian process models to data and to make predictions with them. We will also explore their applications in geostatistics, optimization and reinforcement learning. 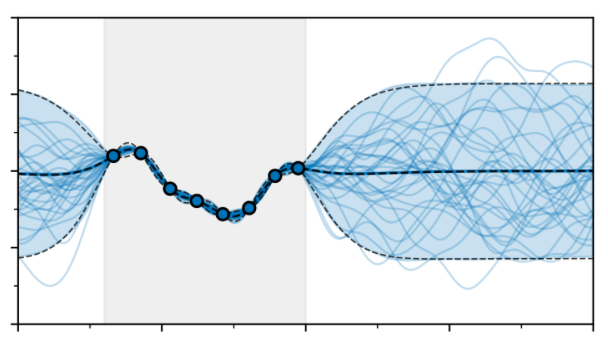
Видеозаписи лекций
По вопросам проведения школы можно обращаться к Дымову Андрею Викторовичу.
- О ВЫШКЕ
- Цифры и факты
- Руководство и структура
- Устойчивое развитие в НИУ ВШЭ
- Преподаватели и сотрудники
- Корпуса и общежития
- Закупки
- Обращения граждан в НИУ ВШЭ
- Фонд целевого капитала
- Противодействие коррупции
- Сведения о доходах, расходах, об имуществе и обязательствах имущественного характера
- Сведения об образовательной организации
- Людям с ограниченными возможностями здоровья
- Единая платежная страница
- Работа в Вышке
- ОБРАЗОВАНИЕ
- Лицей
- Довузовская подготовка
- Олимпиады
- Прием в бакалавриат
- Вышка+
- Прием в магистратуру
- Аспирантура
- Дополнительное образование
- Центр развития карьеры
- Бизнес-инкубатор ВШЭ
- Образовательные партнерства
- Обратная связь и взаимодействие с получателями услуг
-
http://www.minobrnauki.gov.ru/
Министерство науки и высшего образования РФ
-
https://edu.gov.ru/
Министерство просвещения РФ
-
http://www.edu.ru
Федеральный портал «Российское образование»
-
https://elearning.hse.ru/mooc
Массовые открытые онлайн-курсы
- © НИУ ВШЭ 1993–2026 Адреса и контакты Условия использования материалов Политика конфиденциальности Карта сайта
- Редактору





